|
经过拉氏变换,可得到振动方程的频域表达式
其中,{F(s)}为激励向量,{x(s)}为响应向量。 令s=jω,然后引入模态坐标,令{x(s)}=[φ]{q},[φ]为振型矩阵,[q]为模态坐标,则式(2)可以表示为
相互耦合的N自由度系统的方程组经正交变换,成为模态坐标下相互独立的N个自由度系统的方程组,解耦后的第i个方程为
从式(4)中可知,在采用模态坐标后N自由度系统的响应相当于在N个模态坐标下单自由度系统的响应之和。将模态质量归一化振型记为φ,采用归一方法使模态质量归一,即得
可得, 1.2 齿轮装配体模态分析理论 上述经典的线性模态分析理论,它要求刚度矩阵[K]是不变化的。刚度矩阵[K]是和约束有关系的,约束不同计算出的[K]不同,固有频率也不同。齿轮啮合传动时轮齿之间相互接触,存在约束关系。由于啮合部位和接触面积是随时间变化的,所以这种约束关系是随时间变化的,即[K]是时变的,也就是说齿轮传动系统并不存在一个确定的固有频率,不符合传统的线性模态分析理论。 |
基于SolidWorks和ANSYS某舵机齿轮装配体模态分析(2)
时间:2015-08-10 16:04来源:未知 作者: 点击:
次
------分隔线----------------------------





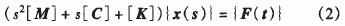
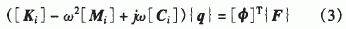
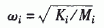
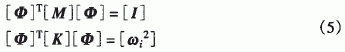
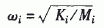 为模态固有频率。
为模态固有频率。