有限元法是当今解决工程问题和数学物理问题中应用最广泛的数值计算方法，它具有对复杂几何构形的适应性和对各种物理问题的可应用性，建立在严格理论上的可靠性和适合计算机实现的高效性等特点，现在已经发展成为CAD和CAM的重要组成部分之一。

目前广泛使用有限元方法对齿轮进行的特性分析，主要是在静态下对单一齿轮进行的研究，很少有考虑齿轮的高速旋转以及啮合时轮齿之间相互约束的影响。作者分别对齿轮进行了静止状态分析与高速旋转状态下的模态分析。通过比较可知，齿轮的固有频率、振型、振幅在工作状态下发生了很大的改变。对于某小型无人机舵机的传动系统，通常是在高速和频繁变速的工况下工作，传统的单一齿轮静态线性模态分析方法不能满足分析的需要，故对齿轮系统进行实际工况下的振动分析就显得很有意义。

1 有限元模态分析理论

1.1 模态分析基本理论

模态分析的本质就是将物理模型转化成模态模型。模态分析需要已知结构的几何形状、边界条件和材料特性，把结构的质量分布、刚度分布和阻尼分布，分别用质量矩阵、刚度矩阵和阻尼矩阵表示出来，通过这些信息来确定系统的模态参数，进而完整地描述系统的动力学特征。

根据有限元法，得到齿轮系统的运动微分方程

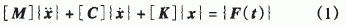
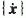式中，[M]、[C]和[K]分别为系统质量矩阵、阻尼矩阵和刚度矩阵；{x}、和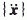分别为位移向量、速度向量和加速度向量；{F(t)}为外力向量。